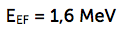DETERMINAÇÃO DA ENERGIA EFETIVA DE UM FEIXE CONTÍNUO DE RAIOS X PARA RADIOTERAPIA

Fausto Mafra Neto, Arnie Verde Nolasco, André Lima de Souza Castro

Físicos do Instituto de Radioterapia São Francisco -  Belo Horizonte,  MG - Brasil

janeiro de 2017

RELATÓRIO

Introdução

Na primeira metade do século XX, a medicina praticou uma radioterapia construída com base no 226Ra, com as bombas de radium e a braquiterapia, e nas máquinas de raios X com potencial acelerador de até 200 ou 250 kV. Naquela ocasião foi dominante, em nosso meio, a escola inglesa de Manchester dirigida pelo médico Dr. Ralston Paterson.

As máquinas de raios X ofereciam um serviço que, naquela época era denominado terapia profunda, uma vez que atingiam cerca de 70% da dose superficial na profundidade de 5cm, num campo de 100cmˆ2.(DELARIO, 1953; JOHNS et al, 1974) 

Grande parte, da dose prescrita, era absorvida na pele e, em geral, causava efeitos indesejados, em razão da predominância de fótons de baixa energia.  

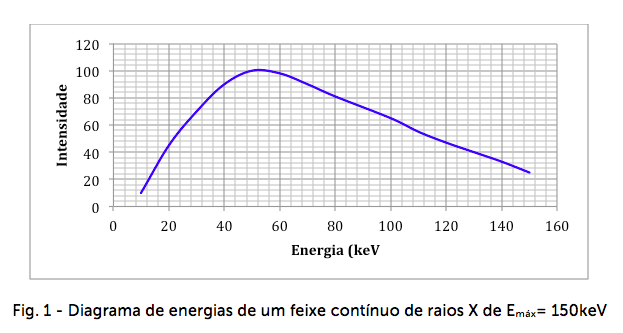
O espectro de energias do feixe é uma função contínua do comprimento de onda das emissões e, pode ser representado graficamente como função da energia em keV como está mostrado na figura 1.

A construção desta curva, para uma determinada máquina, é um procedimento de alta complexidade, e necessita de escaner multicanal com detector especial para esse fim. Exige experiência nesse tipo de medida, particularmente por se tratar de feixe de Alta Taxa de Dose, sem falar na indisponibilidade desse instrumento.

Observa-se na figura 1, a predominância de uma determinada energia. É parte de nossa atividade profissional, determinar esse valor ao qual denominamos energia efetiva, que é a representação da qualidade do feixe.

A energia efetiva corresponde a energia de um feixe monoenergético capaz de produzir o mesmo efeito que o feixe contínuo e que tem a mesma camada semirredutora, CSR (ou HVL), isto é a espessura de um material que reduz a intensidade do feixe à metade e que representamos por d1/2

Geometria experimental

A grandeza camada semirredutora é uma forma experimental e prática de relatar a energia efetiva do feixe de raios X. Pode ser medida utilizando qualquer material de fácil trato e de fácil obtenção, e de preferência, de pureza conhecida.

A determinação da energia efetiva, em MeV, ocorre neste mesmo procedimento considerando que a intensidade I medida na câmara dedal obedece à relação:

em que d é a espessura da lâmina atenuadora e μ é o coeficiente linear de atenuação, característico do material utilizado, para cada energia.

A camada semirredutora é uma característica do feixe contínuo de raios X, e, portanto, não poderá contar com a radiação espalhada. Neste trabalho foram tomados cuidados que garantissem a leitura única do feixe primário. Os seguintes equipamentos e parâmetros físicos foram utilizados:

                                                  câmara de ionização tipo dedal de 0,6cm³;

                                                  capa de equilíbrio eletrônico para a câmara;

                                                   distância foco-câmara eletiva - 80cm;

                                                  campo 3 x 4 cm² para comportar a câmara dedal;

                                                  raio central do feixe no centróide da câmara.

Medidas com o feixe livre

Neste experimento foram utilizadas lâminas de chumbo, encontradas no comercio metalúrgico, de 1mm de espessura nominal, (elemento 5 da figura 2) e os resultados estão mostrados na tabela 1.

Determinação dos coeficientes de atenuação

A figura 3 é a representação gráfica da função exponencial descrita pela equação 1 e obtida experimentalmente. Se fizermos I = Io/2, na equação 1, encontraremos o ponto da curva correspondente à camada semi-redutora, d1/2.

O valor de d1/2 deve ser determinado matematicamente no processo de linearização da função exponencial. 

Se aplicarmos o logarítmo neperiano dos dois lados da equação 1, o resultado será uma função linear representada pela equação 2:

em que o μ e o lnIo são coeficientes a determinar. A figura 4 é a representação gráfica da função logarítmica

  Consideramos aqui a densidade do chumbo ρ = 11,3g/cm3 e, portanto o nosso coeficiente massivo de atenuação obtido é:

A energia efetiva pode ser encontrada com aplicação do método de interpolação de Newton (método das diferenças divididas) aos resultados encontrados na tabela 2. 

Uma interpolação menos rigorosa encontra o valor abaixo, resultado bem satisfatório para fins didáticos.

Energia de um feixe modificado

Nos procedimentos terapêuticos atuais, quase sempre fazemos uso de dispositivos como bandejas acrílicas, filtros compensadores, etc, os quais modificam o feixe original. 

No caso das bandejas, efetuamos uma correção na unidade monitor com um fator que denominamos fator de bandeja. Para os filtros compensadores, essa solução não basta, em razão da modificação que ocorre na configuração das curvas de isodoses e nas percentagens da dose profunda, como acontece com os filtros em cunha de cobre e barreiras para transmissão parcial.

Qual deve ser a variação da energia efetiva de um feixe de raios X bloqueado por um elemento metálico, em relação ao feixe aberto?

Ao feixe de raios X estudado no ítem 4, para o qual medimos uma energia efetiva de 1,4 MeV, vamos interpor um bloqueio de cerrobend com 1cm de espessura, como é visto na figura 6, o elemento 7.

Medidas com o feixe bloqueado

As leituras realizadas no eletrômetro foram tomadas com utilização das mesmas lâminas de chumbo de 1,0mm de espessura. A câmara dedal permanece na mesma posição com a capa de equilíbrio eletrônico.

Do processo de regressão, aplicado à função linear da figura 8, encontramos os coeficientes constantes da equação 

Retornando à interpolação na tabela 2, encontramos a energia efetiva 

Conclusão

Enquanto perdurou o uso dos raios X de ortovoltagem, os livros didáticos de física das radiações ofereceram dados técnicos para obtenção da energia efetiva (DELARÍO, A. J. , 1953). O mesmo não acontece hoje com os feixes contínuos de alta energia, milhão de eletron volts. Os livros didáticos atuais não oferecem esses recursos sob alegação de que as camadas semi-redutoras são muito próximas, tornando-se menos indicadas para relatar a qualidade de um feixe. Diversas alternativas tem sido oferecidas para controle da energia como é o caso das TPR20/10 e das DAPR20/10 utilizadas para a dosimetria nos protocolos de IMRT (NPL, 2015) e para campos muito pequenos.  Esses números, como o HVL, são úteis para o controle diário, ou semanal, ou mensal da reprodutibilidade da energia do feixe.

Entendemos que, qualquer que seja o método que conduza ao valor verdadeiro da energia, esse valor deve ser conhecido e registrado. A interposição do bloqueio de 1cm de cerrobend como na figura 6 responde pelo aumento de 14% na energia efetiva do feixe medido na figura 2.

Bibliografia

DELARÍO, A. J. Roentgen, Radioisotope Therapy – Lea & Febiger – Philadelphia, 1953

GLASSTONE S. y SESONSKE A. Nuclear reactor Engineering – Editorial Reverté – Barcelona, 1975

GRODSTEIN, G. W., National Bureau of Standards, Circular 583, 1957.

JOHNS, H. E., CANNINGHAM, J. R., The Physics of Radiology – Charles C Thomas, Publisher, Springfield Illinois, 1974.

LAMARSH, J. G. Introduction to Nuclear Engineering – Addison Wesley Publishing Company – Massachusetts, 1975.

MASSEY, J. B. Manual de Dosimetría en Radioterapia: Coleccion de Informes Tecnicos no 110 – Organismo Internacional de Energia Atomica – Viena, 1971.

PODGORSAK E. B. – Radiation Oncology Physics: a Handbook for Teachers and Students – IAEA – Viena 2005.

www.NPL-National Physical Laboratory: Application of Dose Area Product and DAP Ratio to Dosimetry in IMRT. Julho de 2015.

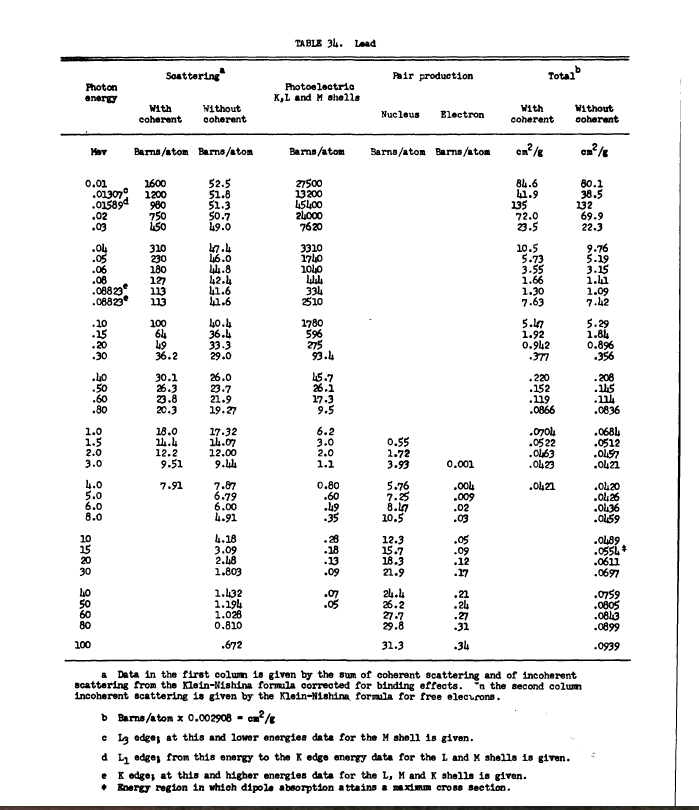
Anexos - Grodstein, G. W. - X ray Atenuation Coeficients from 10keV to 100 MeV

Anexo 1

Anexo 2

Anexo 3

Anexo 4